We are often struck by how often we spend time trying to optimize something, when we are better off choosing a better algorithm. There is an old story about the mathematician Gauss when, in school, he was given the hectic task of adding integers from 1 to 100. While the other students diligently added up each number, Gauss realized that 100+1 is 101 and 99 + 2 is also 101. Guess what 98+3 is? Of course, 101. So you can easily find that there are 50 pairs that add up to 101 and know that the answer is 5,050. No matter how fast you can add, you're unlikely to beat someone who knows that algorithm. So here's a question: You have a large piece of text and you want to search for it. What is the best way?
Of course, this is a loaded question. Best can mean many things and will depend on what kind of data you are working with and even what type of machine you are using. If you're only looking for a single string, you can certainly do a brute force algorithm. Let's say we're looking for the word "guilty" in the text of War and Peace:
- Start with the initials of War and Peace
- If the current letter is not the same as the current letter of "Guilty," go to the next letter, reset the current letter to "Guilty," and go back to step 2 until there are no more letters.
- If the current letters are the same, move to the next letter of the offender and compare it with the next letter, without forgetting the current letter of the text. If it's the same, keep repeating this step until there are no more letters in "guilty" (at which point you have a match). If it is not, reset the current letter of "guilty" and also go back to the original current letter of the text and then move to the next letter, going back to step 2.
It's really hard to describe it in English. But, in other words, just compare the text with the search string, character by character until you find a match. It works and, in fact, with some modern hardware you can write some pretty fast code for that. Can we do better?
better algorithm
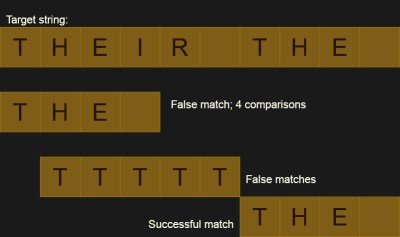
Again, it really depends on your definition of better. Let's say there are several strings in the text that are almost exactly what we're looking for, but not quite. For example, there are probably many occurrences of the word "the" in War and Peace. But there are also "there," "then," and "others," all of which contain our target word. It's not a big deal for the word "the" as it is short, but what if you were going through large search strings? (I don't know - DNA genome data or something.) You'll spend a lot of time chasing dead ends. It's going to be frustrating when you find that the current text contains 199 of the 200 characters you're looking for.
There is one more disadvantage. While it is easy to tell where the string matches and, therefore, where it does not match, it is difficult to detect whether the mismatch has resulted in only a small insertion or deletion. This is important for devices like diff And rsync Where they don't want to know what matches, they want to understand why things don't match.
Was looking rsyncIn fact, it inspired me to see how rsync Compares two files using a rolling checksum. While it may not be for every application, it is something interesting to have in your bag of tricks. Obviously, one of the best uses of this "rolling checksum" algorithm is how rsync uses it. That is, it detects when files are separated very quickly, but can also do a fair job of detecting when they are identical. By rolling the frame of reference, rsync It can detect whether something was inserted or removed and make appropriate changes remotely, saving network bandwidth.
in search of
However, you can use the same strategy to handle large text searches. To do this, you need a hashing algorithm that can easily insert and remove items. For example, suppose the checksum algorithm was dead simple. Simply add together the ASCII code for each letter. So the string "AAAB" is 65 + 65 + 65 + 66 or 261. Now suppose the next character is a C, which is "AAABC". We can calculate the checksum starting from the second by subtracting A(65) first and adding C(67). Of course, silly with this small data set, but instead of adding hundreds to the number every time you want to calculate the hash, you can now do it with an addition and subtraction.
Then we can calculate the hash for our search string and start computing the hash of the file for the same length. If the hash codes do not match, we know there is no match and we move on. If they match, we probably need to verify the match because hashes are usually infallible. The hash value of two strings can be the same.
However, it has some problems. If you're only looking for a single string, the cost of computing the hash is expensive. In the worst case, you'll have to do a comparison, an addition and a subtraction for each character, plus some tests for when you have a hash collision: two strings with the same hash that don't exactly match Huh. With the general scheme, you only need to do one test for each character plus a few pointless tests for false positives.
To optimize the hash algorithm, you can do hardcore hashing. But it's even more expensive to compute, making the overhead worse. However, what if you were looking for a bunch of similar strings of equal length? Then you can calculate the hash once and save it. Each subsequent quest will be much faster because you won't waste time investigating many dead ends, only backwards.
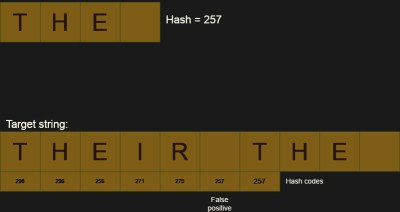
My hash algorithm is very simple, but not very good. For example, you can see in the example that there is a false positive which will lead to additional comparisons. Of course, better hash algorithms exist, but the potential for collisions is always there.
How much difference is there in using this hashing strategy? well i decided write a little code to find out, I decided to ignore the search pattern hash and the cost of computing the initial part of the rolling hash as they would zero out over enough interactions.
Convicted
If you search for the word "guilty" in a text on War and Peace from Project Gutenberg, you'll find that it occurs only four times in the 3.3 million characters. A typical search took about 4.4 million comparisons to figure it out. The hash algorithm easily wins with just under 4.3 million. But the hash calculation ruins it. If you count the addition and subtraction as the same cost of the two comparisons, that adds up to about 5.8 million pseudo-comparisons in total.
Is it special? There probably aren't too many false positives for "guilty". If you run code with the word "the" that should have a lot of false hits, the traditional algorithm has about 4.5 million comparisons and the total adjusted for the hash algorithm is about 9.6 million. So you can see how false positives affect the general algorithm.
You will note that my weak hashing algorithm results in a large number of false hash positives which destroy some of the benefits. A more complex algorithm would help, but would also cost some advance calculation, so it doesn't help as much as you might think. Almost any hashing algorithm for an arbitrary string will have some collisions. Of course, for short search strings, the hash could be the search string and would be correct, but it is not possible in the general case.
The code doesn't save the hash, but let's say it did and assume that the false positive rate of the first search is about the average. This means that we save over 100,000 comparisons per search once the hash is pre-computed. So once you have to search for 60 or so strings, you break even. If you search for 600 strings - but don't forget that they should all be the same size - you can save quite a bit on easy comparison code.
I didn't really time things, because I didn't want to optimize every bit of code. In general, fewer operations are going to be better than more operations. There are lots of ways to increase the efficiency of the code and there are also some approximations you can apply if you analyze the search string a bit. But I just wanted to verify from my gut-level experience how much each algorithm spent on finding the text.
some ideas
I originally started thinking about this after reading the code for rsync and backup programs kup, Turns out there's a name for it, Rabin-Karp algorithm, There are some better hash functions that can reduce false positives and have a few extra points of efficiency.
What's my point? I'm not suggesting that rk search is your best approach for things. You really need a large data set with lots of fixed size searches to take advantage of this. if you think something like rsync, it is actually using the hash to search for places where two very long strings may be equal. But I think there are cases where these oddball algorithms can make sense, so it's worth knowing about them. It's also fun to challenge your intuition by writing a little code and getting some guesses as to how much better or worse one algorithm is than the other.

0 Comments